中3数学って計算から始まりますよね。
そして、みんなやる気があるんですぐ出来るようになるんですよ。
「できるできる〜」って言いながらノリノリで勉強してくれるんですが、引っかかるんですよね。
平方根
たしかに平方根の計算自体はクリアしてくれる生徒が多いのですが、
\(\sqrt{20n}\) が整数となる自然数nのうち、最も小さい数を求めなさい。
これに引っかかるんですよ。
「まず何言ってるか分からない」
…て思うじゃないですか。
これ、実はすごい簡単なので、今日ここで理解していっちゃって下さい。
contents
とりあえず正解が分かればいい方へ
確かに理解は重要ですが、期限が迫っていたり、とにかく急がないといけない場合も想定して「とりあえず正解を出す方法」を紹介します。
- \(\sqrt{54n}\)
- \(\sqrt{\frac{54}{n}}\)
を整数にする自然数nを求める。
上のようにルートの中にnがかけ算や分数で入っているものであれば、以下の方法で簡単に答えられます。
- 数字を素因数分解する
- 同じ数字が2個あったら取り除く
- 残ったものを答えにする(複数余ったらかけ算)
これだけです!
具体的にやってみます
\(\sqrt{54n}\) が整数となる自然数\(n\)のうち、最も小さい数を求めなさい。
- STEP.1数字を見て素因数分解する

今回の数字は54なので、54を素因数分解します。
\(54=2\times3\times3\times3\) ですね。
- STEP.2同じ数字が2個あったら取り除く

今回は3が3個ありますが、2個ずつで考えるので、3を2個だけ取り除きます。
- STEP.3残ったものを答えにする
残った数字は2と3が1個ずつですね。残った数字が2つ以上あったら全部をかけ算です!
ということで\(2\times3=6\)を答えにします。
答え:\(n=6\)
仮に問題の意味が分からなくても、素因数分解ができれば答えられます!
では続いて分数の方も…と行きたいのですが、実は全く同じです。
つまり\(\sqrt{\frac{54}{n}}\)を整数にするnを知りたかったら、
- 54を素因数分解する
- \(54=2\times3\times3\times3\)
- 2つある3を除外して答えは\(2\times3=6\)
です。
形が違っても答え方は同じになるのです。
繰り返しになりますが、この問題で重要なのは素因数分解ですね!
ではここからは、なぜそれで答えになるのか、確認していきます。
理解して、ちょっと違った問題でも簡単に答えられるようになってしまいましょう!
●自然数とは
自然数は数の一種で、正の整数のことです。
ただ言葉の通り「自然に使う数」を表します。
具体的には1や5や100などですね。
逆にマイナスの数字や小数、分数は自然数ではありません。
買い物を頼まれたとき「牛乳0.15パック買ってきて」とか「たまごマイナス5個」とか言われませんよね。
そういう意味で自然な数が自然数です。
なんでそうなるか解説
上の方法で一応解き方だけは知っていただけたかと思います。
これで大抵の問題は解けるのですが、ちょっとひねった問題になったときにできなかったり、記憶が曖昧になったときに確かめられなかったりします。
ということでここからは、理屈も含めて解説していきます。
→解説よりもトレーニングがしたいという方はこちら!

様々なパターンの問題が作成できます。(しかも問題は毎回変わります!)
その前にそもそも平方根って?
その前に平方根の意味について確認しておくと
2乗してその数になる数のうち、プラマイが同じ方
たとえば\(\sqrt{3}\)→2乗して3になる数の、プラスの方
→だいたい1.7(\(1.7\times1.7=2.89\))
→書き表せないので\(\sqrt{3}\)としてる
です。
説明はいろいろあると思いますが、あいまいな方はこれで理解して下さい。
これで、平方根の確認ができたところで、本題の「ルートのついた数に○○したら整数になる自然数」を考えていきます。
ルートの付く数字は無理数と言って、小数でも書ききれない数です。
だからルートがつくのですが、大体いくつか(近似値)は覚えておくと便利となります。
\(\sqrt{2}=1.4\)とする」みたいに書かれますしね
「ルートのついた数に○○したら整数になる自然数」
例題で解説していきます。
理屈が分かれば応用も効くようになるのでガンバって下さい!
\(\sqrt{54n}\) が整数となる自然数\(n\)のうち、最も小さい数を求めなさい。
この問題のポイントは
「\(\sqrt{54n}\) が整数となる」
の理解です。
まず、整数になるとは?
そもそも\(\sqrt{54n}\) はルートがついているので整数ではありません。
じゃあどうなったら整数になるのか
→数字が全部ルートの外に出ればいいんです!
(ルートがない数になればいいんです!)
では、「ルートの外に出る」のはどういうときか
→ルートの中身が何かの2乗になっているときです!
→nが自由に決められるので、ルートの中身が何かの2乗になるようにn調節すればいい!
たとえば\(\sqrt{9}\) は「2乗して9になる数」ですよね。
ところで「2乗して9になる数」は\(3\)ですよね。
ということで\(\sqrt{9}=3\)です。
●考えないでもできるようになるべきこと
\(\sqrt{9}=3\)のように、ルートの中身が何かの2乗だったらルートを外す!
ここから問題を解いていきます!
ルートのついた数字を整数にするためには、ルート中身を何かの2乗にすればいいことが分かりました。
ここからは「ではどうしたらいいか」を解説していきます。
中身は上に書いたものと同じですが、こちらではちょっとだけ詳しく。
「なぜ素因数分解をするのか」、そこを理解することがポイントです。
\(\sqrt{54n}\) が整数となる自然数\(n\)のうち、最も小さい数を求めなさい。
- STEP.1素因数分解してみる

素因数分解をすると
\(54=2\times3\times3\times3\)となり
\(\sqrt{54}=\sqrt{2\times3\times3\times3}\)と分かります。
- STEP.22乗はルートの外に出す

\(54\)の中には\(3^2\)が含まれていることが分かったので、\(3\)をルートの外に出します。
\(\sqrt{2\times3\times3\times3}=3\sqrt{2\times3}\) - STEP.3残った数字が2乗になるnを考える
問題には\(n\)が入っていましたね。
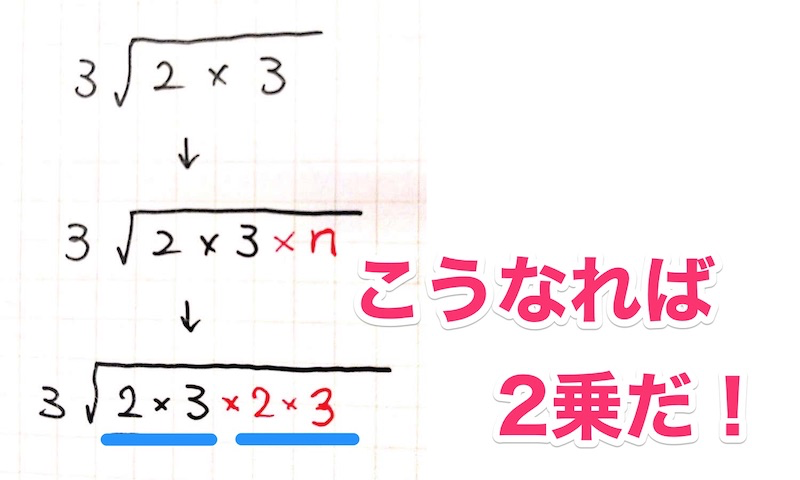
\(3\sqrt{2\times3}→3\sqrt{2\times3\times n}\)ここで、\(n\)が何ならルートの外に出るかを考えるのですが、「ルートの外に出る」=「2乗になっている」です。
つまり、\(n=2\times3\)であれば、ルートの中身が\(2\times3\times2\times3\)となって、\(2\times3\)の2乗になっていると言えます。
結局、素因数分解をしたときに2乗をつくれなかったものが答えになります。
- STEP.4答える\(n=2\times3=6\)
ここまでやって答えです。
というわけで、素因数分解の目的は、「2乗にするためにあと何が必要か?」を知ることです。
そして大抵の場合の問題の答えは、2乗になっていない数字と同じ数字を持ってくることで、2乗にしてあげます。
だから
素因数分解をして→2乗になっていないものが答え
というわけでした。
繰り返しになりますが、「大抵の場合」はこれで答えです。
分数のときも使えます。
ただ、引き算のときは少し違います。
でも、「ルートの中身を何かの2乗にすればいい」と分かっているので、もうできるはずです。
念のため、分数や引き算のパターンの解説もしておきます。
分数だったり引き算があったらどうするか
基本が分かったところで応用問題を勉強します!
応用と言っても「難しい」という意味ではなく「同じ考え方でちょっと違う問題を解く」と思って下さい!
きっとできます!
\(\sqrt{\frac{54}{n}}\)が整数となる自然数\(n\)のうち、最も小さい数を求めなさい。
分数になっても目的は同じです。
ルートの中身を何かの2乗にする
です。
そして、今回は分数なので整数にするために約分を使います。
ではさっそく解いていきます。
- STEP.1やっぱり素因数分解
素因数分解するのは同じです。
\(54=2\times3\times3\times3\)となり今回は
\(\sqrt{\frac{54}{n}}=\sqrt{\frac{2\times3\times3\times3}{n}}\)ですね。
- STEP.22乗はルートの外に
2乗はルートの外側に出します。
書き方が難しいですが
\(=3\sqrt{\frac{2\times3}{n}}\)のようにしておいて下さい。
- STEP.3約分して1にしてしまおう!
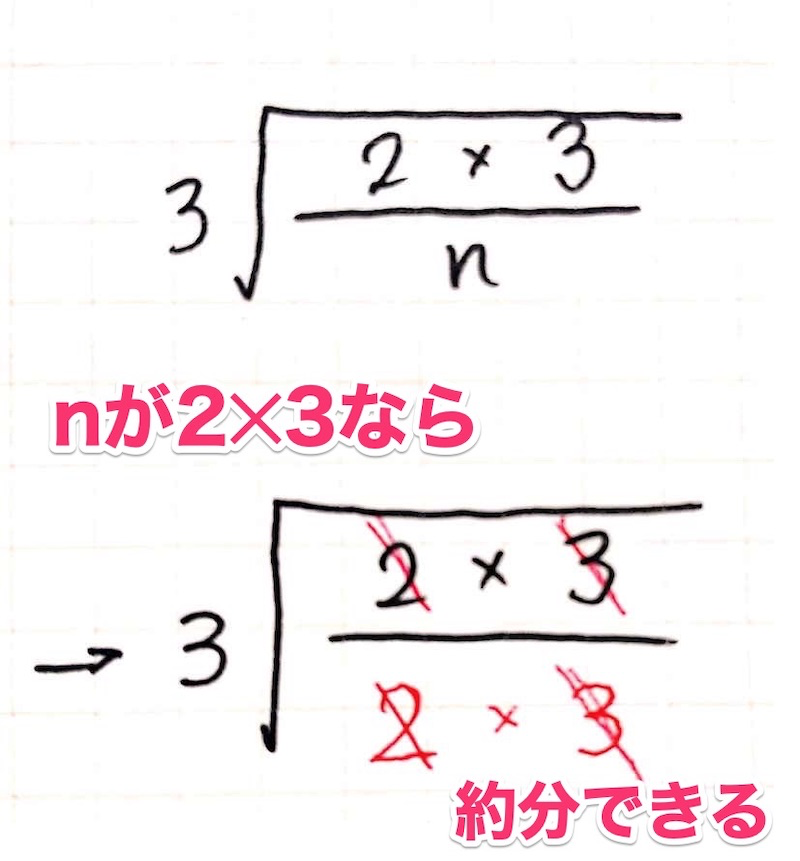
残る\(2\times3\)をどうするかですね。
分数の場合は約分して1にしてしまいましょう!
\(1=1^2\)なので「ルートの中身を何かの2乗にする」目的達成です。
具体的には分母の\(n\)を\(2\times3\)ということにしてしまえば、分子と同じになり約分できます。
- STEP.4掛け算して答えます
あとは答えるだけですね。
\(n=2\times3=6\)よって答えは\(n=6\)でした。
結局上の問題と同じ6でしたね。
ちょっと違う考え方は使っていますが、やっていることは同じなので当然でしょう。
逆に言えば、「整数になる自然数」はかけ算でも分数でも同じやり方できるというわけです。
では次は、ちょっとだけ方法が違う「引き算のパターン」を確認します。
●「3乗になる」だったらどうする
たまーに似た問題で、「自然数\(n\)をかけてある整数の3乗にしなさい」みたいな問題もあります。
今までのルートがついた問題は、「2乗だったらこうやる」というものでした。
それが3乗になっただけなので、今まで「2」や「2つ」でやっていたところを、「3」に変えればいいだけです!
例題を用意してみたので、気になったらやってみて下さい。
\(54n\)がある数の3乗の数となる自然数\(n\)のうち、最も小さい数を求めなさい。
●「最も小さい」について
「ルートのついた式にnをかけて整数にしなさい」「nをかけて何かの2乗にしなさい」のパターンの問題では、
「最も小さい数」
という条件がつく事が多いです。
理由は、実はそうしないと答えが無限にあったりするからです。
たとえば上の「\(\sqrt{\frac{54}{n}}\)が整数となる自然数\(n\)のうち、最も小さい数を求めなさい。」の例では\(n=6\)が答えでした。
ただ、整数にするためには「ルートの中身が何かの2乗になっていればいい」のです。
もし「最も小さい」ルールがない場合にはもともと何かの2乗になっている数、\(6\times2^2=24\)も\(6\times3^2=54\)なども答えになってしまいます。(本当にそうか気になる方は試してみて下さい!)
これだと数字の数だけ答えがあるので、問題として適切じゃないですよね。
というわけで「最も小さい数」という条件がつくのです。
引き算だったらどうするか
引き算のパターンも基本の「ルートの中身を何かの2乗にする」は変わりません。
ただ、引き算で2乗をつくるのでやり方が違います。
つまり、「今ある数字から何を引いたら、2乗の数字になる?」を考えます。
例題でやってみましょう。
\(\sqrt{54-n}\)が整数となる自然数\(n\)のうち、最も小さい数を求めなさい。
- STEP.12乗になる数を考える

引き算のパターンでは素因数分解はしません!
でも目的は同じで「ルートの中身を何かの2乗にする」です。
その何かですが、
- 今回の数字は\(54\)
- そこから引き算で減らしていく
\(54\)より小さい2乗とは?
- \(7\times7=49\)
- \(6\times6=36\)
- \(5\times5=25\)
- …
のどれかだ!と判断します。
- STEP.2方程式をつくってnを調べる
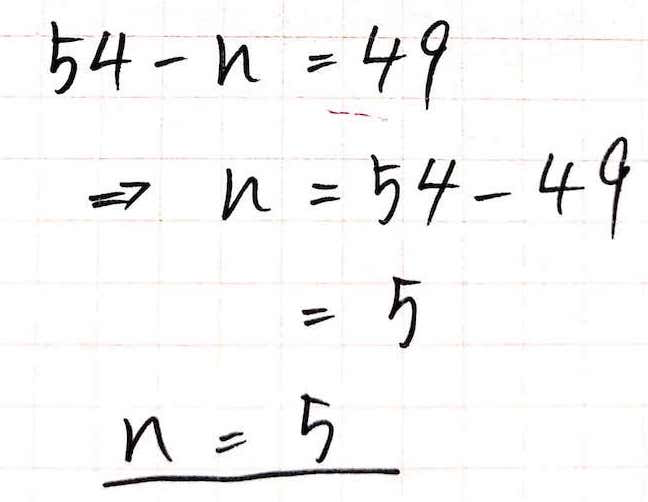
今回の条件は「\(n\)が一番小さくなるとき」です。
なので\(54\)に一番近い\(49\)が一番の候補ですね。
方程式をつくって調べると。
\(54-n=49\)
\(⇒n=54-49=5\)と、\(n\)は\(5\)であると分かりました。
- STEP.3条件を確認して答える
ところで、引き算のパターンでは答えは無限にありません。
ルートの中身が1になるまでです。(2乗すると絶対正の数なのでマイナスはありません。)
そうなると場合によっては「全て答えなさい」というパターンもあります。
その場合には、\(54-n=1\)まで順に試さないといけません。
でも今回は一番小さい数なので、
\(n=5\)でした。
「ルートの中身を何かの2乗にする」問題まとめ
このパターンの問題はとにかく「ルートの中身を何かの2乗にする」です!
あとはとにかく慣れでしょう!
平方根の問題は慣れるまで「これどっちだっけ?」となることが非常に多いんです。
ということで以下の問題をバンバン解いて慣れていって下さい、宿題です( ̄ー+ ̄)